4. Horizontal curve

โค้งวงกลม (Circular Curves)

ความหมาย

   โค้งวงกลมเป็นโค้งรูปแบบพื้นฐานที่สุดที่วิศวกรโยธาควรทราบถึงประโยชน์

ในการใช้งาน การคำนวณหาองค์ประกอบต่างๆ ของโค้ง รวมถึงการกำหนด

ตำแหน่งต่างๆ เพื่อการวางแนวโค้ง ด้วยความที่โค้งวงกลมมีลักษณะที่ง่ายต่อ

การออกแบบ และเป็นพื้นฐานของการวางแนวเส้นทาง

ต่างๆ จึงมีชื่อเรียกอีกชื่อหนึ่งว่า Simple curve

ประโยชน์ของโค้งวงกลม

เพื่อให้ผู้ศึกษาได้เรียนรู้ถึงขั้นตอนในการคำนวณองค์ประกอบต่างๆ ของโค้งวงกลม 

และการกำหนดตำแหน่งขององค์ประกอบเหล่านั้นในภูมิประเทศจริง

การคำนวณโค้งวงกลม

รูปที่ 1 แสดงองค์ประกอบต่าง ๆ ของโค้งวงกลม

จากภาพ

T = ความยาวของเส้นสัมผัสโค้งวงกลมเท่ากับ JQ และ JP

R = รัศมีโค้งวงกลม และตั้งฉากกับเส้นสัมผัสวงกลมตาม

       กฎเรขาคณิต

arc = ความยาวตามแนวโค้ง PQ ที่สามารถวัดหรือคำนวณได้

P, Q = เป็นจุดปลายของโค้งวงกลม

PQ = ความยาวของเส้นคอร์ดของวงกลมเท่ากับ LC

∆ = มุมเห (Intersection) เป็นมุมรองรับส่วนโค้งวงกลม

            ***ข้อควรจำ เมื่อต้องคำนวณเกี่ยวกับโค้งวงกลม คือ เส้นที่ลากจาก

จุดสัมผัสของวงกลมย่อมตั้งฉากกับรัศมีวงกลม และแบ่งครึ่งมุมที่รองรับส่วน

โค้งวงกลมเสมอ 

สูตรการคำนวณหาส่วนต่าง ๆ ของโค้งวงกลม

ความยาวของเส้นสัมผัส (Tangent = T) 

ความยาวของเส้นคอร์ด (Length of Chord = LC)

มุมสัมพันธ์โค้ง (Degrees of curve = D) 

ความยาวของโค้งวงกลม(Length of curve = Lc หรือ arc)

 

ความยาว ณ กึ่งกลางคอร์ดถึงกึ่งกลางโค้ง (Middle ordinate = M)  

ความยาว ณ กึ่งกลางโค้งถึงจุดตัดของเส้นสัมผัส (External distance = E)

ความยาวของรัศมีโค้งวงกลม(Radius of curve = R)

ตัวอย่างการคำนวณโค้งวงกลม

Example:

It is required to connect two intersecting straights whose deflection angle is 

13°16’00” by a circular curve of radius 600m. The through chainage of 

theintersection point is 2745.72m and pegs are required on the centreline 

of the curve at exact multiples of 25m of through chainage.

Tabulate the data necessary to set out the curve by the tangential angles 

method using a theodolite and tape.

Solution:

Through chainage of T = Chainage of I – IT = 2745.72 – 69.78 = 

2675.94mTo fix the first point on the curve at 2700m 

(the next multiple of 25m) the initial sub chord is:

Initial sub-chord = 2700 – 2675.94 = 24.06m

          Length of circular curve = LC = Rθ (θ in radians).

  

Through chainage of U = Chainage of T + LC = 2675.94 

+ 138.93 = 2814.87m Hence a final sub-chord is also 

required since 25m chords can on be used up to 2800m

Length of final sub-chord = 2814.87 – 2800 = 14.87m

Hence the 3 chords necessary are:

การวางโค้งวงกลม

   โค้งวงกลมเป็นโค้งรูปแบบพื้นฐานที่สุดที่วิศวกรโยธาควรทราบถึง

ประโยชน์ในการใช้งาน การคำนวณหาองค์ประกอบต่างๆของโค้ง 

รวมถึงการกำหนดตำแหน่งต่างๆ เพื่อการวางแนวโค้ง ด้วยความที่

โค้งวงกลมมีลักษณะที่ง่ายต่อการออกแบบ และเป็นพื้นฐานของ

การวางแนวเส้นทางต่างๆ จึงมีชื่อเรียกอีกชื่อหนึ่งว่า Simple curve

   ในการปฏิบัติงานจริง ช่างสำรวจจะทำการวางแนวถนนโดยกำหนดจุด

ต่างๆ ไม่ว่าจะเป็นตำแหน่งของจุด POT PI PC และ PT ไวแล้วใน

หน้างาน และกำหนดค่าของ Degree of curve และรัศมีของโค้ง(R)

ไว้แล้วในเบื้องต้นโดยผ่านการเห็นชอบของวิศวกรผู้ควบคุมงาน 

ด้วยเหตุนี้เมื่อนําข้อมูลที่ได้จากสนามมาให้วิศวกรในสำนักงานวิเคราะห์

และออกแบบ ก็จะทราบค่าของมุม Δ (Deflection angle) อยู่ก่อนแล้ว

ในเบื้องต้น 

อย่างไรก็ดีในปฏิบัติการ นี้จะทำการกำหนดค่าพื้นฐานต่างๆที่จำเป็นต่อ

การคำนวณและออกแบบไว้ให้จากนั้นเมื่อนำค่าดังกล่าวมาคำนวณหา

องค์ประกอบต่างๆของโคงวงกลมแล้ว จึงนำสิ่งที่ได้จากการออกแบบไป

ทำการกำหนดตำแหน่งต่างๆของโค้งในภูมิประเทศจริงต่อไป

วัตถุประสงค์

ปฏิบัติการที่ 1 นี้มีวัตถุประสงค์เพื่อให้ผู้ศึกษาได้เรียนรู้ถึงขั้นตอนในการ

คำนวณองค์ประกอบต่างๆของโค้งวงกลม และการกาหนดตำแหน่งของ

องค์ประกอบเหล่านั้นในภูมิประเทศจริง

เครื่องมือ/อุปกรณ์ที่จำเป็น

1. กล้อง Theodolite/กล้องวัดมุม

2. เทปวัดระยะ

3. หมุดเหล็กหรือไม้ตะปู ค้อน และเศษผ้าสำหรับใช้เป็นสัญลักษณ์ให้

มองเห็นโดยสะดวก

4. Pins

5.ขาตั้งกล้อง

6.ปริซึม

7.โพล

8.ลูกน้ำโพล

ขั้นตอนการดำเนินงาน

1.กำหนดตำแหน่งของจุดPI ในสนาม ทำการตอกหมุดที่ตำแหน่งดังกล่าวทำ

สัญลักษณ์ เพื่อให้สามารถมองเห็นได้ชัดเจน

2.นำกล้องไปตั้งที่หมุด PI กำหนดทิศทางและตำแหน่งของจุด PC อย่าง

คราวๆโดยควรเป็นทิศทางที่มีระยะเพียงพอสำหรับตอกหมุดPC เล็งกล้องไป

ในทิศทางดังกล่าว ลากเทปจาก PI ไปตามแนวเล็งโดยใช้ Pin เป็นเป้าเล็งให้

ได้ ระยะเท่ากับ T (Tangent distance)จากนั้นทำการกำหนดจุดPC ในสนาม

3.เล็งกล้องไปยังจด PC จากค่า Deflection angle หมุนกล้องเปิดมุมไปใน

ทิศทางของจุด PT เล็งกล้องไปในทิศทางดังกล่าว ลากเทปจาก PI ไปตาม

แนวเล็งโดยใช้ Pin เป้าเล็งให้ได้ ระยะเท่ากับ T จากนั้นทำการกำหนดจุดPT 

ในสนาม โดยที่หมุด PC และ PT ที่กำหนดขึ้นนั้นควรใช้เศษผ้าสีแดงกำกับไว้

เป็นสัญลักษณ์ เพื่อให้มองเห็นได้ง่าย

4.ย้ายกล้องมาตั้งไว้ที่จุด PC ตั้งระดับแล้วหมุนกล้องส่องจุดPI ตั้งค่าจานองศา

ราบให้เท่ากับศูนย์

5.เปิดมุมกล้องโดยหมุนควงสัมผัสทางราบ (Tangent screw) ให้อ่านมุมได้

เท่ากับ 0 34′07.32′′ (ถ้ากล้องบางชนิดไม่สามารถอ่านค่าวิลิปดาได้ให้ทำเป็น

จุดทศนิยมของลิปดาแทน) วัดระยะตามแนวเล็งกล้องเท่ากับ 5.170 เมตรเรา

จะได้ตำแหน่งของ STA 10+625

6.เปิดกล้องอ่านมุมต่อเนื่องเท่ากับ 3 19′07.32′′  วัดระยะจาก STA 10+625 

เท่ากับ 24.990 เมตร โดยให้แนวลาก ตามระยะดังกล่าวตัดกับแนวเล็งกล้อง

อย่างถูกต้อง เราจะได้ตำแหน่งของ STA 10+650

7.เปิดกล้องอ่านมุมต่อเนื่องอีกเช่นกัน เท่ากับ 6 04′07.32′′ วัดระยะจาก 

STA 10+650 ให้ได้ เท่ากับ 24.990 เมตร ให้แนวลากตามระยะดังกล่าวตัด

กับแนวเล็งกล้อง จะได้ตำแหน่งของ STA 10+675

8.ปฏิบัติตามขั้นตอนดังกล่าวจนถึง PT STA ซึ่งแนวเล็งกล้องกับการวัดระยะ

ตัดแนวเล็งจะต้องตรงกับตำแหน่งของPT STA ที่กำหนดวำแล้วพอดี ถ้าไม่

ตรงแสดงว่าเกิดความผิดพลาดในการปฏิบัติที่ไม่ละเอียดพอ

หมายเหตุ ค่าตัวเลขที่ใช้เป็นตัวอย่างในการบรรยาย สามารถดูได้จากตารางที่ 1.1

ข้อแนะนํา

1.ควรเปิดมุมในการกำหนดตำแหน่งของ Station ต่างๆ บนโค้งโดยใช้กล้อง

ทั้งหน้าซ้ายและหน้าขวา

2.ในการกำหนดตำแหน่งของ Station บนโค้ง ในเบื้องต้นควรทำการวัดระยะ

และเล็งตำแหน่โดยประมาณแล้วทำการตอกหมุดจากนั้นตรวจสอบว่าหมุด

ดังกล่าวอยู่ในระยะเทปและแนวเล็งกล้องหรือไม่แล้วจึงวัดระยะให้ถูกต้องอีก

ครั้งหนึ่งขีดเส้นระยะที่ถูกต้องจากนั้นเล็งกล้องไปตัดกับแนวเส้นที่ขีดบนหัว

หมุดแล้วจึงตอกตะปูไว้ทั่วหมุดเพื่อเป็นสัญลักษณ์

3.ควรอ่านค่ามุมอย่างรอบคอบ โดยความคลาดเคลื่อนที่เกิดขึ้นนี้อาจเกิดจาก

ความละเอียดของกล้องไม่เพียงพอ ทำให้ต้องอ่านค่าความละเอียดเป็นจุด

ทศนิยม หรือโดยการประมาณ เช่น กล้องมีความละเอียดในหน่วยลิปดา

แต่ต้องอ่านค่ามุมที่มีความละเอียดถึงฟิลิปดา เป็นต้น

4.ควรจัดเตรียมตารางข้อมลสําหรับการวางโค้งให้เรียบร้อยก่อนออกไปทำงาน

ในสนาม โดยดูตัวอย่างของรูปแบบ

การจัดเตรียมตารางข้อมูลได้จากตารางที่ 1.1

การวางโค้งวงกลม

โค้งผสม (Compound curve )

รูปที่ 1 โค้งผสม

ความหมาย

โค้งที่ประกอบด้วยโค้งวงกลมหลายโค้งมาต่อกัน และจุดศูนย์กลางของโค้งทั้งหมดจะอยู่ด้านเดียวกันของเส้นสัมผัส และเส้นรัศมีของโค้งที่เชื่อมต่อกันจะยาวไม่เท่ากัน

ประโยชน์ของโค้งผสม

1. ใช้ในบริเวณที่มีสภาพภูมิประเทศเป็นภูเขา, เขตพื้นที่ชุมชนที่ไม่สามารถวางแนวทางด้วยโค้งชนิดอื่น เพื่อให้แนวทางมีความเหมาะสมและเขากับสภาพภู มิประเทศ ทั้งนี้เพื่อความปลอดภัยในการขับขี่ยวดยาน

2. ใช้ในบริเวณ Loop ของทางแยกต่างระดับ (Interchange Loops) หรือใช้ในทางขึ้น-ลงทางด่วน (Ramp)

3. ใช้ในเลนเลี้ยว กรณีที่ถนนสายหลักกับถนนสายรองมาตัดกันเนื่องมาจากรถที่อยู่บนถนนสายหลักจะค่อนข้างใช้ความเร็วสูง ดังนั้นเวลาจะเลี้ยวเข้าถนนสายรองการชะลอความเร็วจะต้องใช้ระยะมาก เพื่อป้องกันไม่ให้รถคันหลังที่ตามมาเกิดอุบัติเหตุ

องค์ประกอบต่างๆของโค้งผสม

รูปที่ 2 เรขาคณิตของโค้งผสม

PC = จุดเริ่มต้นโค้ง (Point of Curve)

PT = จุดสุดท้าโค้ง (Point of Tangent)

PI,V = จุดตัดของเส้นสัมผัส (Point of Intersection)

Iหรือ Δ = มุมเห (Angle of Intersection)

PCC จุดต่อของโค้งประกอบทั้งสอง

TL,T1 = เส้นสัมผัสเส้นยาวหรือเส้นสัมผัสของโค้งแรก

TS,T2 = เส้นสัมผัสเส้นสันหรือเส้นสัมผัสของโค้งสอง

PI1,PI2 หรือV1,V2 = PIย่อยของโค้งผสม

I1,I2 หรือ Δ1,Δ2 = มุมเหย่อยของโค้งร่วม 

Lc1,Lc2 = ความยาวโค้งของโค้งร่วม

L1,L2 = ความยาวคอร์ดของโค้งร่วม

L =  ความยาวคอร์ดจาก PCถึงPT

R1 = รัศมีของโค้ง1

R2 = รัศมีของโค้ง2

ประเภทของโค้งผสม

1.โค้งผสมชนิด 2จุดศูนย์กลาง (Two center compound curve)

รูปที่ 3 โค้งผสมชนิดสองจุดศูนย์กลาง

2.โค้งผสมชนิด 3จุดศูนย์กลาง (Three center compound curve)

 

รูปที่ 4 โค้งผสมชนิดสามจุดศูนย์กลาง

3.โค้งผสมชนิด 4 จุดศูนย์กลาง (Fourcenter compound curve)

สูตรที่ใช้ในการคำนวณ (กรณีโค้งผสมสองจุดศูนย์กลาง)

รูปที่ 5 ส่วนประกอบโค้งผสมชนิดสองจุดศูนย์กลาง

การวางโค้งผลม

            วัตถุประสงค์

ปฏิบัติการนี้ มีวัตถุระสงค์เพื่อให้ผู้ศึกษาได้เรียนรู้การวางโค้งในกรณีที่การวางแนวถนน

จำเป็นต้องตัดผ่านภูมิประเทศที่มีลักษณะเฉพาะ เช่น ภูเขา ป่าทึบ หมู่บ้าน ซึ่งต้องการการ

วางโค้งและลักษณะของโค้งที่กลมกลืนกับภูมิประเทศมากกว่าการใช้โค้งวงกลมทั่วๆไป

            เครื่องมือ/อุปกรณ์ที่จำเป็น

1. กล้อง Theodolite

2. เทปวัดระยะ

3. หมุดเหล็ก หรือไม้ตะปูค้อน และเศษผ้าสำหรับใช้เป็นสัญลักษณ์ให้มองเห็นโดยสะดวก

4. Pins

ขั้นตอนการดำเนินงาน 
            1.กำหนดตำแหน่งของจุดPIในสนาม ตั้งกล้องที่จุดPI กำหนดทิศทางและตำแหน่งของ

จุดPCอย่างคร่าวดำเนินการกำหนดจุดPC ในทำนองเดียวกันกับที่เคยทำมาแล้ว เมื่อได้ทิศทาง

ของจุดPCแล้วลากเทปจากกล้องเป็นระยะทางVV1 จะได้ตำแหน่งของจุดV1 วัดระยะต่อมาอีก

เท่ากับT1 จะได้ตำแหน่งของจุดPC 

2.เปิดมุมเท่ากับΔ ด้วยกล้องหน้าซ้ายและหน้าขวาไปในทิศทางของจุดPT ลากเทปจากกล้อง

เป็นระยะทางVV2 จะได้ตำแหน่งของจุดV2วัดระยะต่อมาอีกเท่ากับT2 จะได้ตำแหน่งของPT 

3.ยกกล้องมาตั้งที่จุดPI1 หมุนกล้องส่องไปยังจุดPC เปิดมุมเท่ากับΔ1 ด้วยกล้องหน้าซ้ายและ

หน้าขวา วัดระยะทางเท่ากับT1 ตามแนวเล็งกล้อง จะได้ตำแหน่งของจุดPCC ถ้าทำการวางแนว

ต่อไปจะต้องเข้าหมุดV2พอดี เป็นการตรวจสอบว่าได้วางแนวต่างๆได้ถูกต้องแล้ว   

4.ย้ายกล้องมาตั้งที่จุดPC หมุนกล้องส่องจุดPI ตั้งองศากล้องให้เป็นศูนย์ จากนั้นทำการวางโค้ง

เหมือนโค้งวงกลมทุกประการจนถึงจุดPCC 
           5.ย้ายกล้องไปตั้งที่จุดPCC หมุนกล้องส่องไปที่จุดPI1 ตั้งองศากล้องเท่ากับศูนย์ กระดกกล้อง

ไปทางจุดPI2 
          6.ทำการวางโค้งเหมือนการวางโค้งวงกลมทุกประการจนถึงจุดPT 

โค้งกลับทิศ (Reverse curve)

 

ความหมาย

ตามปกติโค้งผสมจะมีจุดศูนย์กลางอยู่ข้างเดียวกัน แต่ในกรณีที่โค้งผสมมีจุดศูนย์กลางอยู่

ตรงข้ามกันนั้น เราเรียกโค้งดังกล่าวว่าโค้งกลับทิศ หรือ Reverse curve โค้งกลับทิศจะประกอบ

ด้วยโค้งสองโค้งโดยมีจุดร่วม หรือ PRC (Point of reverse curve) หรือมีเส้นสัมผัสร่วมที่ต่อ

เชื่อมกันระหว่างโค้งเรียกว่า Intermediate tangent โค้งกลับทิศมักใช้ในภูมิประเทศที่เป็นภูเขา

 หรือในเขตเมืองที่ไม่สะดวกต่อการรื้อถอนและเวนคืน

ประโยชน์ของโค้งกลับทิศ

โค้ง กลับทิศมักใช้ในภูมิประเทศที่เป็นภูเขา หรือในเขตเมืองที่ไม่สะดวกต่อการรื้อถอนและเวียนคืน

 จะสามารถลดผลกระทบที่จะเกิดต่อสิ่งแวดล้อมน้อย

องค์ประกอบต่างๆของโค้งกลับทิศ

Elements of Reversed Curve 

PC = point of curvature

PT = point of tangency

PRC = point of reversed curvature

T1 = length of tangent of the first curve

T2 = length of tangent of the second curve

V1 = vertex of the first curve

V2 = vertex of the second curve

I1 = central angle of the first curve

I2 = central angle of the second curve

Lc1 = length of first curve

Lc2 = length of second curve

L1 = length of first chord

L2 = length of second chord

T1 + T2 = length of common tangent measured from V1 to V2

ประเภทของโค้งกลับทิศ  

โค้งผสมมีหลายประเภทตามคุณสมบัติขององค์ประกอบโค้งที่แตกต่างกันดังต่อไปนี้ 

1.โค้งกลับทิศที่มีจุดเชื่อมต่อกันที่ จุด PRC 

2.โค้งกลับทิศที่มีเส้นสัมผัสขนานกัน

             2.1. เส้นสัมผัสขนานกันและรัศมีเท่ากัน

 

2.2    เส้นสัมผัสขนานกันแต่รัศมีไม่เท่ากัน

3.โค้งกลับทิศทีเส้นสัมผัสไม่ขนานกันแต่รัศมีเท่ากัน

3.1 AB ได้จากการวางแนวกำหนดมุม α, β หา Δ1 และ Δ2

           3.2   AB ได้จากการวางแนวกำหนด θ, T1, และ R หา Δ1, Δ2 และ T2

การวางโค้งกลับทิศ

            วัตถุประสงค์

ปฏิบัติการที่มีวัตถุระสงค์เพื่อให้ผู้ศึกษาได้เรียนรู้การวางโค้งกลับทิศซึ่งถือได้ว่าเป็น

โค้งผสมประเภทหนึ่ง สำหรับนำไปประยุกต์ใช้ในการวางโค้งในภูมิประเทศที่มีอุปสรรค 

เช่น หุบเขา หรือพื้นที่อาคารที่ไม่เหมาะสม ถ้าจะทำการรื้อถอน เป็นต้น

            เครื่องมือ/อุปกรณ์ที่จำเป็น

1. กล้อง Theodolite

2. เทปวัดระยะ

3. หมุดเหล็ก หรือไม้ตะปูค้อน และเศษผ้าสำหรับใช้เป็นสัญลักษณ์ให้มองเห็นโดยสะดวก

4. Pins

ขั้นตอนการดำเนินงาน

การวางโคงกลับทิศกรณีที่มีจุดเชื่อมต่อกันที่จุด PRC นั้นมีขั้นตอนการดำเนินงานเหมือนกับ

การวางโค้งผสมทุกประการ เพียงแต่ในการปฏิบัติจริงนั้นจะต้องกำหนดเส้นสัมผัสรวมให้ได้ก่อน 

นั้นหมายความว่าในเบื้องต้น จะต้องกำหนดตำแหน่งของจุดV₁ PRC และ V₂ 

แนวปฏิบัติเช่นเดียวกันกับการวางโค้งวงกลม และโค้งผสมตามที่ได้อธิบายไปแล้วในปฏิบัติการ

ก่อนหน้านี้

โค้งก้นหอย (Spiral curve,Transition curve)

ความหมาย 

โค้งก้นหอย หรือ Spiral curve เป็นการออกแบบโค้งเพื่อให้ยวดยานสามารถวิ่งเข้าโค้งได้ด้วย

ความเร็วสูง โค้งก้นหอยสามารถเรียกอีกชื่อหนึ่งว่า Transition curve เนื่องจากลักษณะของโค้ง

เป็นโค้งราบ สามารถนำไปต่อกับโค้งอื่นๆ หรือนำมาต่อกันเองได้ โดยในการออกแบบขะใช้โค้ง

ตั้งแต่หนึ่งโค้งขึ้นไป นิยมใช้โค้งก้นหอยกับถนนหรือทางรถไฟ ที่ต้องการให้ยวดยานเคลื่อนที่

ด้วยความเร็วสูง ใช้แทนโค้งอัตราย(Sharp curve) ทางเลี้ยว ทางแยกต่างระดับ (Interchange)   

และทางแยก (Intersection)  ช่วยให้คนขับสามารถค่อยๆบังคับรถให้เลี้ยวได้ง่าย ใขณะที่ใช้

ความเร็วสูง ทำให้รถไม่เสียหลัก

 

ประโยชน์ของโค้งก้นหอย 

1.ใช้แทนโค้งอันตราย ทางแยก ทางโค้งอันตราย 
2.ช่วยให้คนขับรถสามารถบังคับรถให้เลี้ยงได้ง่าย ขณะที่ใช้ความเร็วสูงทำให้รถไม่เสียหลัก 

 

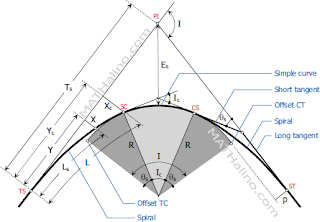
องค์ประกอบต่างๆของโค้งก้นหอย

 

 

    TS = Tangent to spiral
    SC = Spiral to curve
    CS = Curve to spiral
    ST = Spiral to tangent
    LT = Long tangent
    ST = Short tangent
    R = Radius of simple curve
    Ts = Spiral tangent distance
    Tc = Circular curve tangent
    L = Length of spiral from TS to any point along the spiral
    Ls = Length of spiral
    PI = Point of intersection
    I = Angle of intersection
    Ic = Angle of intersection of the simple curve
    p = Length of throw or the distance from tangent that the circular curve has been offset
    X = Offset distance (right angle distance) from tangent to any point on the spiral
    Xc = Offset distance (right angle distance) from tangent to SC
    Y = Distance along tangent to any point on the spiral
    Yc = Distance along tangent from TS to point at right angle to SC
    Es = External distance of the simple curve
    θ = Spiral angle from tangent to any point on the spiral
    θs = Spiral angle from tangent to SC
    i = Deflection angle from TS to any point on the spiral, it is proportional to the square of its 

distance
    is = Deflection angle from TS to SC
    D = Degree of spiral curve at any point
    Dc = Degree of simple curve

แนวคิดของโค้งก้นหอย

1.แนวคิดทางกลศาสตร์
โค้งก้นหอยแรกเริ่มเป็นโค้งก้นหอยในอุดมคติที่ได้แนวคิดมาจากหลักการทางกลศาสตร์ คือ 

การเกิดแรงหนีศูนย์กลาง
2. แนวคิดทางเรขาคณิต
2.1. แนวคิดลดรัศมี ของโค้งวงกลม(R) ลงเท่ากับ P 

 

 

2.2. แนวคิดเลื่อนโค้งวงกลมลงมาโดยที่ โค้งไม่เปลี่ยนแปลงเลย(Shift circular curve)

2.3. แนวคิดให้รัศมีโค้งและองศาโค้งเหมือนเดิม และจุดศูนย์กลางคงที่แต่เลื่อนเสนสัมผัสโค้ง

วงกลมออกไป (Shift tangent line)

 

2.4. เนื่องจากโค้งวงกลมเดิมเป็นโค้งอันตราย จึงเปลี่ยนเป็นโค้งผสมเพื่อให้สามารถใส่ 

Spiral curve ได้

การหาส่วนต่างๆของโค้งก้นหอย

การวางโค้งก้นหอย

วัตถุประสงค์

ฝึกฝนการคำนวณองค์ประกอบของโค้งและวางแนวโค้งที่มีลักษณะเป็นโค้งก้นหอย เพื่อเพิ่ม

ทักษะในการวางโค้งที่มีความซับซ้อนมากยิ่งขึ้น

เครื่องมือ/อุปกรณ์ที่จำเป็น 
        1. กล้อง Theodolite
        2. เทปวัดระยะ
        3. หมุดเหล็ก หรือไม้ตะปูค้อน และเศษผ้าสำหรับใช้เป็นสัญลักษณ์ให้มองเห็นโดยสะดวก
        4. Pins

ขั้นตอนการดำเนินงาน

1.ตั้งกล้องไปที่จุด POT ในทิศทางของจุดTS วัดระยะเท่ากับความยาวเส้นสัมผัส Ts ไปตามแนว

เล็ง จะได้ตำแหน่งของจุด TS จากนั้นวัดระยะย้อนกลับมาเป็นระยะLT จะได้ตำแหน่งของจุด SPI

2. ที่จุดPIs เช่นเดียวกัน หมุนกล้องส่องจุด POT ในทิศทางของจุดST วัดระยะตามแนวเล็งให้

เท่ากับความยาวของเส้นสัมผัสTs จะได้ตำแหน่งของจุด ST เมื่อวัดย้อนกลับมาเท่ากับระยะLT 

จะได้ตำแหน่งของจุด SPI

3. ย้ายกล้องไปตั้งที่จุด SPI หมุนกล้องส่องปังจุดPIs ตั้งค่าองศากล้องเท่ากับศูนย์ เปิดมุมโค้ง

ก้นหอย θs วัดระยะเท่ากับST จะได้ตำแหน่งของจุดSC หรือ CS

4. เราอาจทำการตรวจสอบตำแหน่งของจุดSC หรือCS ได้ด้วยค่า Xc หรือ Yc ที่คำนวณไว้อีกครั้ง

ก็ได้ วัดระยะSC-CS จะได้ค่าเท่ากับความยาวคอร์ดของโค้งวงกลม

5. ทำการวางโค้ง จากจุดTS โดยตั้งกล้องที่จุดTS จากนั้นเล็งกล้องไปที่จุด PIs ตั้งค่าองศากล้อง

เท่ากับศูนย์ แล้วดำเนินการ เปิดมุม แล้ววัดระยะคอร์ดเพื่อหาตำแหน่งSTAต่างๆ ทำไปเรื่อยจนถึง

จุดSC

Horizontal curve part 1

Horizontal curve part 2

ที่มา :   http://www.surames.com/images/column_1236244868/Lab_7.pdf

http://www.surames.com/images/column_1236244868/Compound%20curve.pdf

             http://www.mathalino.com/reviewer/surveying/compound-and-reversed-curves

             http://www.surames.com/images/column_1236244868/Reverse%20curve%20and%20Spiral%20curve.pdf

             http://www.surames.com/images/column_1236244868/Lab_9.pdf